问题
单项选择题
设f(x)为微分方程y'=xy=g(x)满足y(0)=1的解,而
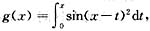 则( )
则( )
答案
参考答案:B
解析:
[分析]: 利用微分方程可求f'(0),f"(0)及f'"(0)等,从而确定x=0是否为极值点或(0,f(0))是否为拐点。
[详解] 由y'-xy=g(x),[*]知g(0)=0,从而y'(0)=0。
又 y"=y+xy'+g'(x)=y+xy'+sinx2,
于是 y"(0)=y(0)=1
可见y=f(x)在点x=0处取极小值
故应选(B)
[评注] 不一定将微分方程的解求出来,直接利用微分方程的关系式进行分析即可。
