问题
解答题
我们知道,顺次连接任意四边形各边中点所得四边形是平行四边形,那么顺次连接等腰梯形各边中点所得四边形是什么特殊四边形呢?探索并证明你的结论.
答案
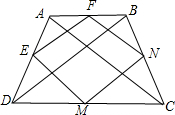
是菱形.
如图,梯形ABCD,AD=BC,且点E,F,M,N,分别是四边形的中点,则四边形EFMN是菱形.
证明:∵四边形ABCD是等腰梯形,且点E,F,M,N,分别是四边形的中点,
∴EF=MN=
BD,FN=EM=1 2
AC,1 2
∵梯形ABCD,AD=BC,
∴AC=BD,
∴EF=MN=FN=EM,
∴四边形EFMN是菱形.
