下列命题正确的是( ).
A.设
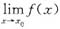 不存在,
不存在,
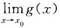 存在,则
存在,则
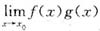 必存在.
必存在.
B.设
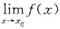 不存在,
不存在,
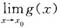 不存在,则
不存在,则
 必不存在.
必不存在.
C.设
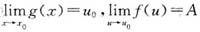 ,则必有
,则必有
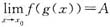 .
.
D.设
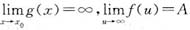 ,则必有
,则必有
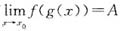 .
.
参考答案:D
解析:
[分析]: 方法一 证明(D)是正确的.由[*],对于任给ε>0,存在M>0,当|u|>M时,有|f(u)-A|<ε.又因[*],故对于上述M>0,存在δ>0,当0<|x-x0|<δ时,|g(x)|>M.将上述两点结合起来推知,对于任给ε>0,存在δ>0,当0<|x-x0|<δ时,有|f(x)-A|<ε,即
[*]
(D)正确.
方法二 用排斥法.(A)的反例:[*]不存在g(x)x,n[*]存在.但[*]仍不存在.
(B)的反例:[*]不存在.[*]亦不存在.但
[*],(存在).
(C)的反例:[*].
[*]
但对于复合函数[*],不论δ>0多么小,在x=0的δ去心邻域Uδ(0)={x|0<|x|<δ)内,f(g(x))在无穷多个点处(例如[*],n=1,2,…)没有定义(因分母为0),因此谈不上取极限[*],(C)也不成立,故选(D).