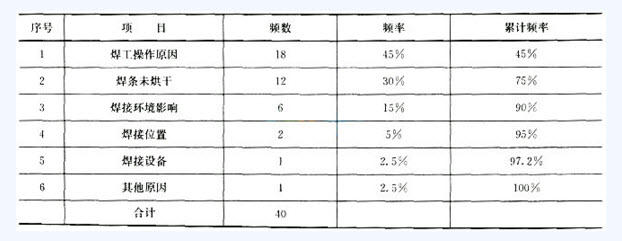
某城市地下工程,业主与施工单位参照FIDIC合同条件签订了施工合同,除税金外的合同总价为8600万元,其中:现场管理费率15%,企业管理费率8%,利润率5%,合同工期730天。为保证施工安全,合同中规定施工单位应安装满足最小排水能力1.5t/min的排水设施,并安装1.5t/ min的备用排水设施,两套设施合计15900元。合同中还规定,施工中如遇业主原因造成工程停工或窝工,业主对施工单位自有机械按台班单价的60%给予补偿,对施工单位租赁机械按租赁费给予补偿(不包括运转费用)。
该工程施工过程中发生以下三项事件。
事件1:施工过程中业主通知施工单位某分项工程(非关键工作)需进行设计变更,由此造成施工单位的机械设备窝工12天。
事件2:施工过程中遇到了非季节性大暴雨天气,由于地下断层相互贯通及地下水位不断上升等不利条件,原有排水设施满足不了排水要求,施工工区涌水量逐渐增加,使施工单位被迫停工,并造成施工设备被淹没。
为保证施工安全和施工进度,业主指令施工单位紧急增加购买额外排水设施,尽快恢复施工,施工单位按业主要求购买并安装了两套1.5t/min的排水设施,恢复了施工。
事件3:施工中发现地下文物,处理地下文物工作造成工期拖延40天;
就以上三项事件,施工单位按合同规定的索赔程序向业主提出索赔。
事件1:由于业主修改工程设计12天,造成施工单位机械设备窝工费用索赔见表4-1所示。
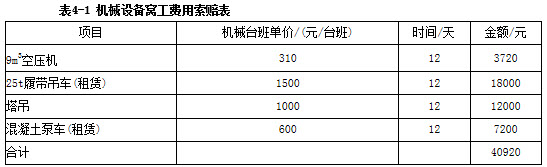
现场管理费:40920元×15%=6138元
企业管理费:(40920+6138)元×8%=3764.64元
利润:(40920+6138+3764.64)元×5%=2541.13元
合计:53363.77元
事件2.由于非季节性大暴雨天气费用索赔:
(1)备用排水设施及额外增加排水设施费:(15900÷2×3)元=23850元
(2)被地下涌水淹没的机械设备损失费16000元
(3)额外排水工作的劳务费8650元
合计:48500元
事件3.由于处理地下文物,工期、费用索赔:
延长工期40天
索赔现场管理费增加额:
现场管理费:8600万元×15%=1290万元
相当于每天:(1290×10000÷730)元/天=17671.23元/天
40天合计:(17671.23×40)元=706849.20元
[问题]
1.指出事件1中施工单位的哪些索赔要求不合理,为什么造价工程师审核施工单位机械设备窝工费用索赔时,核定施工单位提供的机械台班单价属实,并核定机械台班单价中运转费用分别为:9m3空压机为93元/台班,25t履带吊车为300元/台班,塔吊为190元/台班,混凝土泵车为 140元/台班,造价工程师应核定的索赔费用应是多少?
2.事件2中施工单位可获得哪几项费用的索赔核定的索赔费用应是多少?
3.事件3中造价工程师是否应同意40天的工期延长为什么补偿的现场管理费如何计算,应补偿多少元?