问题
选择题
在△ABC中，角A、B、C的对应边分别为x、b、c，若满足b=2，B=45°的△ABC恰有两解，则x的取值范围是（ ）
|
答案
由三角形有两角的充要条件可知xsin45°＜b＜x，
即
x＜2＜x，2 2
解得2＜x＜2
，2
即x的取值范围是（2，2
）．2
故选：C．
搜题请搜索小程序“爱下问搜题”
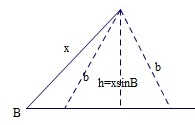
在△ABC中，角A、B、C的对应边分别为x、b、c，若满足b=2，B=45°的△ABC恰有两解，则x的取值范围是（ ）
|
由三角形有两角的充要条件可知xsin45°＜b＜x，
即
x＜2＜x，2 2
解得2＜x＜2
，2
即x的取值范围是（2，2
）．2
故选：C．
①体会自己点点滴滴的进步，学会为自己喝彩
②采用场景变换等方式，寻找自己的优点和长处
③在任何事情上都不要落于人后
④避免犯任何错误
A．①②③
B．①③④
C．①②
D．③④