问题
解答题
(1)已知点B(6,0)和C(-6,0),过点B的直线l与过点C的直线m相交于点A,设直线l的斜率为k1,直线m的斜率为k2,如果k1•k2=-
(2)用正弦定理证明三角形外角平分线定理:如果在△ABC中,∠A的外角平分线AD与边BC的延长线相交于点D,则
|
答案
(1)设A点坐标为(x,y),可得直线的斜率为k1=
,y x-6
直线m的斜率为k2=
,y x+6
结合题意可得
•y x-6
=-y x+6
,整理得4 9
+x2 36
=1(x≠±6)y2 16 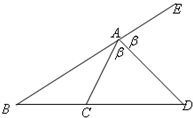
所以点A的轨迹是以B、C为焦点的椭圆(除长轴端点除外).
(2)设∠CAD=∠DAE=β,
在△ACD中,由正弦定理得
=DC sinβ
…①,AC sin∠D
在△ABD中,由正弦定理得
=BD sin∠BAD
,即AB sin∠D
=BD sin∠β
…②①②两式相除,可得AB sin∠D
=BD DC
,结论成立.AB AC
