如图,以Rt△ABC的直角边AC. BC向形外作正方形ACGH. 正方形CBEF,连结GE. AE
求证:(1)AE=GE;(2)EC垂直平分AG。
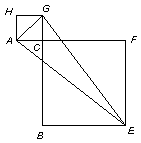
| 证明:(1)连结CE ∵四边形ACGH、CBEF是正方形 | |
| ∴AC=CG,∠CFE=∠BCF=45° | |
| ∵∠ACB=∠QCF=90°∴∠ACE=∠GCE | |
| ∵CE=CE ∴△ACE≌△GCE | |
| ∴AE=GE | |
| (2)∵AC=CG,AE=GE | |
| ∴C、E都在线段AG的中垂线上 ∴CE垂直平分AG | 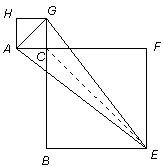 |
如图,以Rt△ABC的直角边AC. BC向形外作正方形ACGH. 正方形CBEF,连结GE. AE
求证:(1)AE=GE;(2)EC垂直平分AG。

| 证明:(1)连结CE ∵四边形ACGH、CBEF是正方形 | |
| ∴AC=CG,∠CFE=∠BCF=45° | |
| ∵∠ACB=∠QCF=90°∴∠ACE=∠GCE | |
| ∵CE=CE ∴△ACE≌△GCE | |
| ∴AE=GE | |
| (2)∵AC=CG,AE=GE | |
| ∴C、E都在线段AG的中垂线上 ∴CE垂直平分AG |  |