It’s really true what people say about English politeness: it’s everywhere. When squeezing (挤过去) past someone in a narrow passage, people say “sorry”. When getting off a bus, English passengers say “thank you” rather than the driver. In Germany, people would never dream of doing these things. After all, squeezing past others is sometimes unavoidable, and the bus driver is only doing his job. I used to think the same way, without questioning it, until I started traveling to the British Isles, and here are some more polite ways of interacting (交往) with people in UK.
People thank each other everywhere in England, all the time. When people buy something in a shop, customer and shop assistant in most cases thank each other twice or more. In Germany, it would be exceptional to hear more than one thank you in such a conversation. British students thank their lecturers when leaving the room. English employers thank their employees for doing their jobs, as opposite to Germans, who would normally think that paying their workers money is already enough.
Another thing I observed during my stay was that English people rarely criticize (批评) others. Even when I was working and mistakes were pointed out to me, my employers emphasized several times but none of their explanations were intended as criticism. It has been my impression that by avoiding criticism, English people are making an effort to make others feel comfortable. This also is showed in other ways. British men still open doors for women, and British men are more likely to treat women to a meal than German men. However, I do need to point out here that this applies to English men a bit more than it would to Scottish men! Yes, the latter are a bit tightfisted.
小题1:What is the author’s attitude towards English politeness?
A.He thinks it is unnecessary.
B.He thinks little of it.
C.He appreciates it very much.
D.He thinks it goes too far.小题2:What can be inferred from the passage?
A.German men never treat a woman to dinner.
B.The author think it’s unnecessary to say “thank you” to the bus driver.
C.In Germany, employers often say “thank you” to employees for their job.
D.Germans think it is unnecessary to thank workers because payment is enough.小题3:We can learn from the last paragraph that Scottish men ______.
A.like to fight with each other
B.treat women in a polite way
C.are as generous as English men
D.are unwilling to spend money for women小题4:The author develops the text through the method of ______.
A.making comparisons
B.telling stories
C.giving reasons
D.giving examples

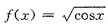 的带皮亚诺余项的五阶麦克劳林公式是______.
的带皮亚诺余项的五阶麦克劳林公式是______.