问题
解答题
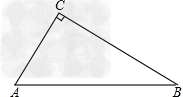
如图,在△ABC中,BC>AC,∠C=90°。
(1)在BC上作点M,使点M到点A,B的距离相等;(要求:尺规作图,保留作图痕迹,不写作法和证明)
(2)当满足(1)的点M到AB,AC两边的距离相等时,求∠B的度数。
答案
解:(1)如图所示:
(2)过点M作AB的垂线,垂足为E,连接AM,
∵点M到AB,AC两边的距离相等,
∴点M在上∠CAB的平分线上,即∠CAM=∠MAB,
又∵ME垂直平分AB,
∴AM=BM,
∴∠MAB=∠B,
∴∠CAM=∠MAB=∠B,
又∵∠C=90°,
∴∠CAM+∠MAB+∠B=180°﹣90°=90°,
即3∠B=90°,∠B=30°。

