问题
解答题
已知圆C经过A（1，-1），B（5，3），并且被直线m：3x-y=0平分圆的面积。
（Ⅰ）求圆C的方程；
（Ⅱ）若过点D（0，-1），且斜率为k的直线l与圆C有两个不同的公共点，求实数k的取值范围。
答案
解：（Ⅰ）线段AB的中点E（3，1），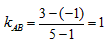
，
故线段AB中垂线的方程为y-1=-（x-3），即x+y-4=0，
由圆C经过A、B两点，故圆心在线段AB的中垂线上，
又直线3x-y=0平分圆的面积，所以直线m经过圆心，
由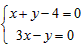
，解得
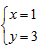，即圆心的坐标为C（1，3），
而圆的半径r=|AC|=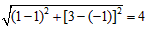
，
故圆C的方程为（x-1）2+（y-3）2=16；
（Ⅱ）由直线l的斜率为k，故可设其方程为y=kx-1，
由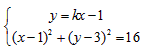
消去y得（1+k2）x2-（8k+2）x+1=0，
由已知直线l与圆C有两个不同的公共点，
故△=（8k+2）2-4（1+k2）＞0，
即15k2+8k＞0，
解得：k＜-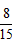
或k＞0。