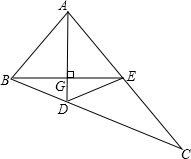
根据题意画出相应的图形，如图所示，

∵AD⊥BE，∴△ABG，△BDG，△EDG，△AGE都为直角三角形，

设AB=c，BC=a，AC=b，

∵D、E分别为BC、AC的中点，

∴BC=

1

2

a，AE=

1

2

b，DE=

1

2

c，

根据勾股定理得：AG²+BG²=c²①，GD²+GE²=

1

4

c²②，

AG²+GE²=

1

4

b²③，BG²+DG²=

1

4

a²④，

（①+②）-（③+④）得：

5

4

c²=

1

4

（a²+b²），即c²=

1

5

（a²+b²），

在△ABC中，cosC=

a2+b2-c2

2ab

=

2

5

•

a2+b2

ab

≥

4

5

，

当且仅当a=b时，cosC最小值为

4

5

，

∵cos（A+B）=-cosC，

∴cos（A+B）的最大值为-

4

5

．

故答案为：-

4

5