问题
证明题
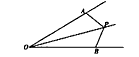
如图所示，P为∠AOB内一点，OA=OB，且△OPA与△OPB面积相等。
求证∠AOP=∠BOP。
答案
证明：过P点分别作PC、PD垂直OA、OB，垂足为C、D，
∵△OPA与△OPB面积相等，
，
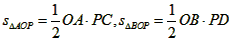即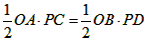
，
又∵OA=OB，
∴PC=PD，
又∵PC⊥OA，PD⊥OB，
∴点P在∠AOB的角平分线上，
∴∠AOP=∠BOP。
搜题请搜索小程序“爱下问搜题”
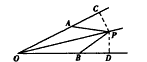
如图所示，P为∠AOB内一点，OA=OB，且△OPA与△OPB面积相等。
求证∠AOP=∠BOP。
证明：过P点分别作PC、PD垂直OA、OB，垂足为C、D，
∵△OPA与△OPB面积相等，
，
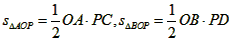即，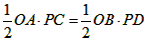
又∵OA=OB，
∴PC=PD，
又∵PC⊥OA，PD⊥OB，
∴点P在∠AOB的角平分线上，
∴∠AOP=∠BOP。