问题
计算题
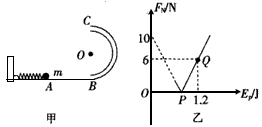
如图甲所示，水平直线导轨AB与竖直面内半径为R的半圆形导轨BC均光滑，在B点相切连接。弹簧被一个质量为m的小球压缩至A点，具有的弹性势能为Ep。现将小球由静止释放，在脱离弹簧后沿水平导轨进入半圆形导轨运动。现用力传感器测出经过C点时小球对轨道的压力FN，改变Ep的大小，可测出相应的FN的大小，FN随Ep的变化关系如图乙所示，试求：（取g=10 m/s2）
(1)小球的质量m和导轨半径R；
(2)说明乙图中P点所代表的物理意义，并求出P点的横坐标。
答案
解：（1）设小球在最高点C时的速度为vC，受到的支持力大小为F
由牛顿第二定律得：mg士F=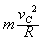
由机械能守恒定律得：Ep=mg·2R+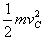
联立解得：F=±(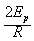
-5mg)
由牛顿第三定律得小球对轨道的压力FN大小为：FN=F=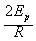
-5mg ①
或FN=F=-(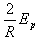
-5mg) ②
由图象截距可知：5mg=10
将Q点坐标代入①式得：6=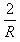
×1.2-5mg
联立解得：m=0.2 kg，R=0.15 m
（2）P点对应于小球对轨道的压力为零，仅有重力提供向心力
在①或②式中，令FN=0，解得：Ep=0.75 J