问题
多选题
一不计质量的直角形支架的两直角臂长度分别为2l和l,支架可绕水平固定轴O在竖直平面内无摩擦转动,支架臂的两端分别连接质量为m和2m的小球A和B,开始时OA臂处于水平位置,如图所示,由静止释放后,则( )
A.OB臂能到达水平位置
B.OB臂不能到达水平位置
C.A、B两球的最大速度之比vA:vB=2:1
D.A、B两球的最大速度之比vA:vB=1:2
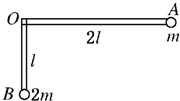
答案
A、B、球A和B系统机械能守恒,可以将AB两球当成一个整体,找出两球整体的质量中心(整体的重心),这样就可以将系统简化为单摆模型,两球整体的质量中心在两个球的连线上,当整体的重心到达最低点时,速度最大,OB杆显然不是水平;
当重心摆到左侧对称位置时,B球最高;假设OB杆能水平,B球重力势能增加2mgl,A球重力势能减小2mgl,机械能守恒,故A正确,B错误;
C、D、由于角速度相等,转动半径固定,根据v=ωr,有
vA:vB=ω?2l:ω?l=2:1
故C正确,D错误;
故选AC.
