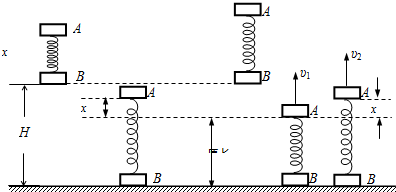
如图所示,将质量均为m厚度不计的两物块A、B用轻质弹簧相连接,只用手托着B物块于H高处,A在弹簧弹力的作用下处于静止,将弹簧锁定.现由静止释放A、B,B物块着地时解除弹簧锁定,且B物块的速度立即变为0,在随后的过程中当弹簧恢复到原长时A物块运动的速度为υ0,且B物块恰能离开地面但不继续上升.已知弹簧具有相同形变量时弹性势能也相同.
(1)B物块着地后,A向上运动过程中合外力为0时的速度υ1;
(2)B物块着地到B物块恰能离开地面但不继续上升的过程中,A物块运动的位移△x;
(3)第二次用手拿着A、B两物块,使得弹簧竖直并处于原长状态,此时物块B离地面的距离也为H,然后由静止同时释放A、B,B物块着地后速度同样立即变为0.求第二次释放A、B后,B刚要离地时A的速度υ2.

(1)设A、B下落H过程时速度为υ,由机械能守恒定律有:2mgH=
2mv21 2
B着地后,A和弹簧相互作用至A上升到合外力为0的过程中,弹簧对A做的总功为零.
即0=
m1 2
-v 21
mv21 2
解得:v1=2gH
(2)B物块恰能离开地面时,弹簧处于伸长状态,弹力大小等于mg,B物块刚着地解除弹簧锁定时,弹簧处于压缩状态,弹力大小等于mg.因此,两次弹簧形变量相同,则这两次弹簧弹性势能相同,设为EP.
又B物块恰能离开地面但不继续上升,此时A物块速度为0.
从B物块着地到B物块恰能离开地面但不继续上升的过程中,A物块和弹簧组成的系统机械能守恒EP+
m1 2
=mg△x+EPv 21
得△x=H
(3)弹簧形变量x=
△x1 2
第一次从B物块着地到弹簧恢复原长过程中,弹簧和A物块组成的系统机械能守恒EP+
m1 2
=mgx+v 21
m1 2 v 20
第二次释放A、B后,A、B均做自由落体运动,由机械能守恒得刚着地时A、B系统的速度为v1=2gH
从B物块着地到B刚要离地过程中,弹簧和A物块组成的系统机械能守恒
m1 2
=mgx+v 21
m1 2
+EPv 22
联立以上各式得v2=
.2gH- v 20
答:(1)B物块着地后,A向上运动过程中合外力为0时的速度υ1为
;2gH
(2)B物块着地到B物块恰能离开地面但不继续上升的过程中,A物块运动的位移△x为H;
(3)B刚要离地时A的速度为v2=
.2gH- v 20