问题
计算题
如图所示，水平路面CD的左侧有一固定的平台，平台上表面AB长s=3 m。光滑半圆轨道AFE竖直固定在平台上，圆轨道半径R=0.4 m，最低点与平台AB相切于A.板长L1=2 m，上表面与平台等高，小物块放在板的最右端，并随板一起向平台运动。当板的左端距离平台L=2 m时，板与物块向左运动的速度v0=8 m/s。当板与平台的竖直墙壁碰撞后，板立即停止运动，物块在板上滑动。已知板与路面的动摩擦因数μ1=0.05，物块与板上表面及轨道AB的动摩擦因数μ2=0.1，物块质量m=1 kg，取g=10 m/s2。
(1)求物块进入圆轨道时对轨道上A点的压力；
(2)判断物块能否到达圆轨道的最高点E。如果能，求物块离开E后在平台上的落点到A的距离；如果不能，则说明理由。
答案
解：（1）物块随车运动撞击平台时的速度v1满足
滑块到A点时的速度v2满足
由牛顿第二定律得：
解得：FN=140 N
故滑块对轨道压力大小140 N，方向竖直向下
（2）设物块能通过圆轨道的最高点，且在最高点处的速度为v3，则有
解得：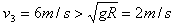
故能通过最高点，做平抛运动，有x=v3t及
解得：x=2.4 m