∵∠BAC=60°，

∴∠ABC+∠ACB=180°-60°=120°，

∵BE、CE分别为∠ABC、∠ACB的平分线，

∴∠EBC=

1

2

∠ABC，∠ECB=

1

2

∠ACB，

∴∠EBC+∠ECB=

1

2

（∠ABC+∠ACB）=

1

2

×120°=60°，

∴∠BEC=180°-（∠EBC+∠ECB）=180°-60°=120°，故①正确；

如图，过点D作DF⊥AB于F，DG⊥AC的延长线于G，

∵BE、CE分别为∠ABC、∠ACB的平分线，

∴AD为∠BAC的平分线，

∴DF=DG，

∴∠FDG=360°-90°×2-60°=120°，

又∵∠BDC=120°，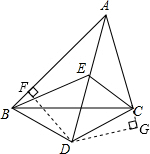

∴∠BDF+∠CDF=120°，∠CDG+∠CDF=120°，

∴∠BDF=∠CDG，

∵在△BDF和△CDG中，

∠BFD=∠CGD=90° DF=DG ∠BDF=∠CDG

，

∴△BDF≌△CDG（ASA），

∴DB=CD，

∴∠DBC=

1

2

（180°-120°）=30°，

∴∠DBE=∠DBC+∠CBE=30°+∠CBE，

∵BE平分∠ABC，AE平分∠BAC，

∴∠ABE=∠CBE，∠BAE=

1

2

∠BAC=30°，

根据三角形的外角性质，∠DEB=∠ABE+∠BAE=∠ABE+30°，

∴∠DBE=∠DEB，

∴DB=DE，故②正确；

∵DB=DE=DC，

∴B，C，E三点在以D为圆心，以BD为半径的圆上，

∴∠BDE=2∠BCE，故③正确；

综上所述，正确的结论有①②③共3个．

故选D．