问题
多选题
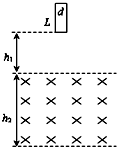
质量为M、内壁间距为L的箱子静止于光滑的水平面上,箱子中间有一质量为m的小物块,小物块与箱子底板间的动摩擦因数为μ.初始时小物块停在箱子正中间,如图所示.现给小物块一水平向右的初速度v,小物块与箱壁碰撞N次后恰又回到箱子正中间,且与箱子保持相对静止.设碰撞都是弹性的,则整个过程中,以下说法正确的是( )
A.物块损失的动能为
mv21 2
B.系统损失的动能为1 2
v2mM m+M
C.系统产生的内能为
mv21 2
D.系统产生的内能为NμmgL

答案
设物块与箱子相对静止时共同速度为V,则由动量守恒定律得
mv=(M+m)V,得V=mv M+m
A、物块损失的动能为△Ek=
mv2-1 2
mV2<1 2
mv2.故A错误.1 2
B、系统损失的动能为△Ek系=
mv2-1 2
(M+m)V2=1 2
.故B正确.Mmv2 2(M+m)
C、根据能量守恒定律得知,系统产生的内能等于系统损失的动能,则有Q=
.故C错误.Mmv2 2(M+m)
D、根据功能关系得知,系统产生的内能等于系统克服摩擦力做的功,则有Q=NμmgL.故D正确.
故选BD