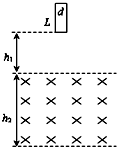
如图所示,一质量为m=0.016kg、长L=0.5m、宽d=0.1m、电阻R=0.1Ω的矩形线圈,从h1=5m的高处由静止开始下落,然后进入高度为h2(h2>L)的匀强磁场.下边刚进入磁场时,线圈正好作匀速运动.线圈的下边通过磁场所经历的时间t=0.15s.取g=10m/s2
(1)求匀强磁场的磁感应强度B.
(2)求线圈的下边刚离开磁场的瞬间,线圈的加速度的大小和方向.
(3)在线圈的下边通过磁场的过程中,线圈中产生的焦耳热Q是多少?通过线圈的电荷量q是多少?
(1)设线圈刚进入磁场时的速度为v0,则据机械能守恒定律可得:
mgh1=
m1 2 v 20
所以有:v0=
=10m/s2gh1
线框产生的感应电动势为:E=Bdv0,
感应电流为:I=Bdv0 R
线框所受的安培力大小为:F=BdI
则得:F=B2d2v0 R
根据平衡条件可得mg=F,即为:mg=B2d2v0 R
代人数据解得:B=0.4T
(2)因为线圈的下边进入磁场后先做匀速运动,用时为:t1=
=0.05s,L v0
所以线圈做加速运动的时间为:t2=t-t1=0.1s
线圈的下边刚离开磁场的瞬间的速度为:v=v0+gt2=11m/s;
线圈的加速度的大小为:a=
=1m/s2,方向向上.B2d2v-mgR mR
(3)在线圈的下边通过磁场的过程中,线圈中产生的焦耳热为:Q=mgL=0.08J
电量为:q=It=
t=E R
=0.2C△φ R
答:(1)匀强磁场的磁感应强度B为0.4T.
(2)线圈的下边刚离开磁场的瞬间,线圈的加速度的大小为1m/s2,方向向上.
(3)在线圈的下边通过磁场的过程中,线圈中产生的焦耳热Q是0.08J,通过线圈的电荷量q是0.2C.
