问题
计算题
某兴趣小组做了一个电场中的过山车小实验。如图所示的绝缘轨道ABCDF处在竖直向下的匀强电场中，其中倾斜轨道AB和竖直的圆形轨道光滑，水平轨道BCF粗糙，C为圆形轨道的最低点，BC段长为L。现有一个质量为m、带电量为-q的小球，从距水平面BC高h=5.4L处的P点由静止下滑，小球恰能通过竖直圆形轨道的最高点D而作圆周运动。已知小球与水平轨道BCF间的动摩擦因素为μ=0.4，空间所加的电场强度为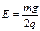
。请问：
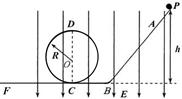
小题1:圆形轨道半径R的大小为多少？
小题2:为使小球不滑出CF，那么水平轨道CF的长度至少为多少？
小题3:现改变h高度，为使小球最终停在B点，请问小球释放点高度h要满足什么要求
？
答案
小题1:R=2L
小题2:12.5L
小题3:0.8L、1.6L、2.4L三个解
⑴恰能过最高点，则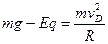
，得到
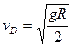（1分）
PD过程动能定理：
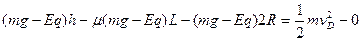（2分）
联立以上两式得到R=2L
(2)小球最终停在CF上，全过程动能定理：
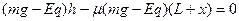（1分）解得x=12.5L（1分）
(3)为使小球停在B点，则小球不能超过1/4圆弧，设到达1/4圆弧速度刚好为零，根据动能定理得到：
，
解得h≤2.8L（2分）
要到达B点，则小球应从圆弧上返回，经偶数次往返运动到达B点速度为0，则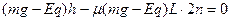
（1分）
得到h=0.8nL(n=1、2、3…) 同时有要满足h≤2.8L
所以取h=0.8L、1.6L、2.4L三个解（1分）