问题
计算题
（2012年2月重庆八中检测）如图所示，可视为质点的总质量（包括装备）为m=60kg的滑板运动员，从高为H=15m的斜面AB的顶端A点由静止开始沿斜面下滑，在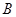
点进入光滑的四分之一圆弧BC，圆弧BC半径为R=5m，运动员经C点沿竖直轨道冲出向上运动，经时间t=2s后又落回轨道。若运动员经C点后在空中运动时只受重力，轨道AB段粗糙、BC段光滑。g=10m/s2。
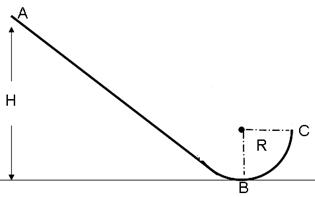
求：（1）运动员在C点的速度和离开C点可上升的高度。
（2）运动员（包括装备）运动到圆轨道最低点B时对轨道的压力大小。
（3）从A点到B点，运动员损失的机械能。
答案
（1）5m（2）3000N（3）3000J
（1）运动员在C点的速度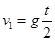
=10m/s，
离开C点可上升的高度h=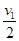
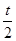=5m。
（2）设运动员运动到圆轨道最低点B时速度为v2，对运动员从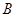
到
：
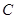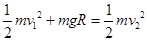（2分）
在最低点B，由牛顿第二定律，F-mg=m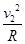
，
解得：F=3000N。
由牛顿第三定律，运动员对轨道的压力大小F’=F=3000N。
（3）从A点到B点，由能量守恒定律，运动员损失的机械能：
△E=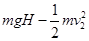
=3000J。