问题
计算题
如图所示,粗糙的斜面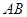 下端与光滑的圆弧轨道
下端与光滑的圆弧轨道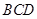 相切于
相切于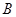 ,整个装置竖直放置,
,整个装置竖直放置, 是最低点,圆心角
是最低点,圆心角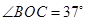 ,
,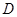 与圆心
与圆心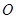 等高.圆弧轨道半径
等高.圆弧轨道半径 0.5 m,斜面长
0.5 m,斜面长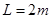 。现有一个质量
。现有一个质量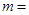 0.1 kg的小物体
0.1 kg的小物体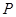 从斜面
从斜面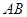 上端
上端 点无初速下滑,物体
点无初速下滑,物体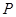 与斜面
与斜面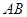 之间的动摩擦因数为
之间的动摩擦因数为 (已知
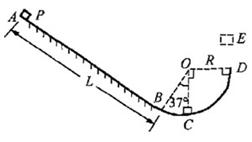
(已知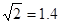 ,g=10m/s2)。求:
,g=10m/s2)。求:
(1)物体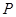 第一次通过
第一次通过 点时的速度大小和对
点时的速度大小和对 点处轨道的压力各为多大?
点处轨道的压力各为多大?
(2)物体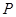 第一次离开
第一次离开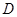 点后在空中做竖直上抛运动,不计空气阻力,则最高点
点后在空中做竖直上抛运动,不计空气阻力,则最高点 和
和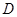 点之间的高度差为多大?
点之间的高度差为多大?
(3)物体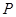 从空中又返回到圆轨道和斜面.多次反复,在整个运动过程中,物体
从空中又返回到圆轨道和斜面.多次反复,在整个运动过程中,物体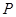 对
对 点处轨道的最小压力为多大?
点处轨道的最小压力为多大?
答案
(1)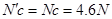 (2)
(2)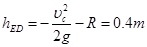 (3)
(3)
题目分析:(1)物体P从A下滑经B到C过程中根据动能定理:
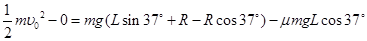 (2分)
(2分)
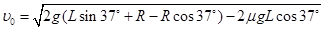
 (2分)
(2分)
经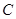 点时
点时 (2分)
(2分)
根据牛顿第二定律,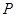 对
对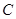 点的压力
点的压力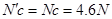 (1分)
(1分)
(2))从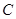 到
到 机械能守恒
机械能守恒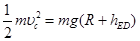 (2分)
(2分)
 与
与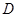 间高度差
间高度差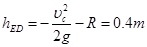 (1分)
(1分)
(3)物体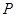 最后在
最后在 与其等高的圆弧轨道上来回运动时,经
与其等高的圆弧轨道上来回运动时,经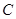 点压力最小,由
点压力最小,由 到
到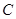 根据机械能守恒
根据机械能守恒
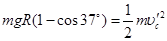
 (2分)
(2分)
 (1分)
(1分)
根据牛顿第三定律 压力 (1分)
(1分)
点评:在考查力学问题时,常常将动能定理、机械能守恒及牛顿第二定律等综合在一起进行考查,并且常常综合平抛、圆周运动及匀变速直线运动等运动的形式.
