问题
计算题
（12分）如图所示，倾角为θ的斜面上只有AB段粗糙，其余部分都光滑，AB段长为3L．有若干个相同的小方块（每个小方块视为质点）沿斜面靠在一起，但不粘接，总长为L．将它们由静止释放，释放时下端距A为2L．当下端运动到A下面距A为L/2时物块运动的速度达到最大．
（1）求物块与粗糙斜面的动摩擦因数；
（2）求物块停止时的位置；
（3）要使所有物块都能通过B点，由静止释放时物块下端距A点至少要多远？
答案
（1）2tanθ (2) 物块的下端停在B端 (3) 3L
题目分析：(1)当整体所受合外力为零时，整体速度最大，设整体质量为m，则
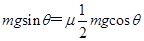2′
得μ＝2tanθ 1′
(2)设物块停止时下端距A点的距离为x，根据动能定理
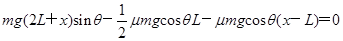2′
解得x＝3L 1′
即物块的下端停在B端 1′
(3)设静止时物块的下端距A的距离为s，物块的上端运动到A点时速度为v，根据动能定理
2′
物块全部滑上AB部分后，小方块间无弹力作用，取最上面一块为研究对象，设其质量为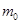
，运动到B点时速度正好减到0，根据动能定理
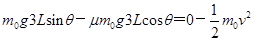2′
得s＝3L 1′
点评：难题。物体在某个运动过程中包含有几个运动性质不同的小过程(如加速、减速的过程)，此时可以分段考虑。本题涉及变力做功，且是随位移均匀变化的，所以可以用算术平均值求变力的功。