问题
计算题
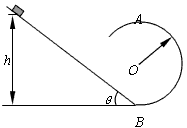
如图所示，倾角θ=37°的斜面底端B平滑连接着半径r=0.40m的竖直光滑圆轨道。质量m=0.50kg的小物块，从距地面h=2.7m处沿斜面由静止开始下滑，小物块与斜面间的动摩擦因数μ=0.25，求：（sin37°=0.6，cos37°=0.8，g=10m/s2）
（1）物块滑到斜面底端B时的速度大小；
（2）物块运动到圆轨道的最高点A时，对圆轨道的压力大小。
答案
解：（1）物块沿斜面下滑过程中，在重力、支持力和摩擦力作用下做匀加速运动，设下滑加速度为a，到达斜面底端B时的速度为v，则
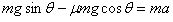①
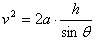②
由①、②式代入数据解得：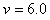
m/s ③
（2）设物块运动到圆轨道的最高点A时的速度为vA，在A点受到圆轨道的压力为N，由机械能守恒定律得：
④
物块运动到圆轨道的最高点A时，由牛顿第二定律得：
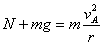⑤
由④、⑤式代入数据解得：N=20N ⑥
由牛顿第三定律可知，物块运动到圆轨道的最高点A时，对圆轨道的压力大小NA=N=20N ⑦