问题
问答题
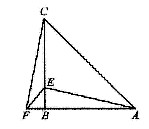
在△ABC中，AB=CB，∠ABC=90°，F为AB延长线上一点，点E在BC上，且AE=CF．
（1）求证：Rt△ABE≌Rt△CBF；
（2）若∠CAE=30°，求∠ACF的度数．
答案
参考答案：
(1)∵∠ABC=90°，
∴∠CBF=∠ABE=90°．
在Rt△ABE和Rt△CBF中有：
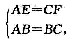
∴Rt△ABE≌Rt△CBF(HL)．
(2)∵AB=BC，∠ABC=90°，
∴∠CAB=∠ACB=45°．
又∵∠BAE=∠CAB-∠CAE=45°-30°=15°，
由(1)知：Rt△ABE≌Rt△CBF，
∴∠BCF=∠BAE=15°，
∴∠ACF=∠BCF+∠ACB=45°+15°=60°．