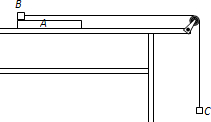
如图所示,长为L的木板A静止在光滑的水平桌面上,A的左端上方放有小物体B(可视为质点),一端连在B上的细绳,绕过固定在桌子边沿的定滑轮后,另一端连在小物体C上,设法用外力使A、B静止,此时C被悬挂着.A的右端距离滑轮足够远,C距离地面足够高.已知A的质量为6m,B的质量为3m,C的质量为m.现将C物体竖直向上提高距离2L,同时撤去固定A、B的外力.再将C无初速释放,当细绳被拉直时B、C速度的大小立即变成相等,由于细绳被拉直的时间极短,此过程中重力和摩擦力的作用可以忽略不计,细绳不可伸长,且能承受足够大的拉力.最后发现B在A上相对A滑行的最大距离为
L.细绳始终在滑轮上,不计滑轮与细绳之间的摩擦,计算中可认为A、B之间的最大静摩擦力等于滑动摩擦力,取重力加速度g=10m/s2.1 2
(1)求细绳被拉直前瞬间C物体速度的大小υ0;
(2)求细绳被拉直后瞬间B、C速度的大小υ;
(3)在题目所述情景中,只改变C物体的质量,可以使B从A上滑下来.
设C的质量为km,求k至少为多大?
(1)C做自由落体运动,下降高度为2L时的速度为v0,根据vt2-v02=2ax得
v0=2gl
(2)此时细绳被拉直,B、C速度的大小立即变成v,设绳子对B、C的冲量大小为I,根据动量定理得
对B I=3mv
对C-I=mv-mv0
解得B、C速度的大小v=gL 2
(3)设C物体的质量为km,A、B之间的动摩擦因数为μ
由(2)可知,细绳被拉直时B、C速度的大小v´=
v0k 3+k
此后B物体的加速度 kmg-μ•3mg=(3m+km)a1
a1=
=kmg-μ•3mg 3m+km
gk-3μ 3+k
A物体的加速度 μ•3mg=6ma2
a2=
=μ•3mg 6m
gμ 2
经时间t,B物体的速度 v1=v'+a1t
B物体的位移 x1=v′t+
a1t21 2
同样,A物体的速度 v2=a2t
A物体的位移 x2=
a2t21 2
(i)根据题意,若k=1,当v1=v2时,x1-x2=
,解μ=0.4;L 2
(ii)要使v1=v2时,x1-x2=L,利用(i)求得的动摩擦因数μ,
可得k=
=1.29;9 7
即C物体的质量至少为1.29m时,才可以使B物体从A上滑下来.
