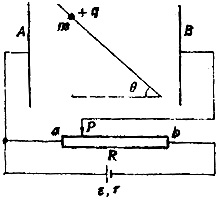
如图,质量m、带电+q的小球套在绝缘杆上,杆与水平面成θ角,球杆间摩擦系数为μ,且有μsinθ>cosθ,杆又放在竖直的平板AB之间,AB间距离为d,并和变阻器及电源相连,变阻器总电阻为R,电源内阻为r.求:
(1)当滑动触头P位于a点时,小球沿杆下滑的加速度为多少?当P由a滑向b时,小球加速度如何变化?
(2)若当P位于变阻器中间时,小球沿杆下滑的加速度恰好达到最大,求这最大加速度值及电源电动势值.
(1)当滑动触头P位于a点时,电容器板间电压为零,板间无电场,小球不受电场力,由牛顿第二定律
得:mgsinθ-μmgcosθ=ma,得 a=g(sinθ-μθ)
当P由a滑向b时,小球受到水平向右的电场力,设为F.
开始阶段,Fsinθ<mgcosθ,杆对球的弹力垂直杆向上,大小为N=mgcosθ-Fsinθ,小球的加速度为a=
=gsinθ-mgsinθ-μN m
(mgcosθ-Fsinθ),P由a滑向b时,F增大,则可知,加速度逐渐增大;后来阶段,Fsinθ>mgcosθ,杆对球的弹力垂直杆向上,大小为N=Fsinθ-mgcosθ,小球的加速度为a=μ m
=gsinθ-mgsinθ-μN m
(Fsinθ-mgcosθ),F增大时,a减小,所以当Fsinθ=mgcosθ时,加速度最大.故在整个过程中,小球的加速度先增大后减小.μ m
(2)由上分析知,当Fsinθ=mgcosθ时,加速度最大为gsinθ.,而且有 F=mgcotθ.
又F=q
,U=U d
•1 2
ER R+r
联立解得,电源的电动势E=2mgd(R+r)cotθ qR
答:(1)当滑动触头P位于a点时,小球沿杆下滑的加速度为gsinθ.当P由a滑向b时,小球加速度先增大后减小.
(2)小球最大加速度值为gsinθ,电源电动势值为
.2mgd(R+r)cotθ qR
