简单机械的应用
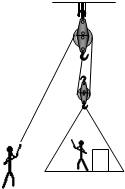
保洁工人要清洗高楼的外墙,他的同伴站在地面上,使用了如图13所示的装置对它进行升降.已知该保洁工的质量为60kg,保洁器材的质量为20kg,他同伴对绳的拉力为500N,吊篮在拉力的作用下1min匀速上升了10m,绳的最大承受拉力为600N,动滑轮和吊篮一共所受的重力为100N,求:
(1)不计摩擦,此滑轮组最多能提起______N的物体.
(2)请你画出吊篮所受力的示意图.
(3)这个滑轮组的机械效率是多大?
(4)小明和同学们还想要了解机械效率与哪些因素有关.为此同学们进行了有关斜面的机械效率的探究.
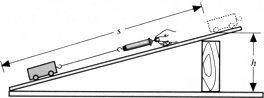
在探究斜面的机械效率时,同学们运用了如图14所示的实验装置,进行了有关实验,并得出如下的结论:如果斜面的光滑程度一样,斜面的长度S和小车的重保持不变,通过改变其高度h的方法测得的机械效率,其机械效率是不同的.
这时有的同学提出:如果保持斜面的高度、长度和光滑程度不变,改变小车的速度、小车的重力,是否会影响它的机械效率呢?
大家积极思考,提出了各种猜想,概括起来有如下几种:
猜想1:可能与匀速拉动的速度大小有关.
猜想2:可能与小车的重力有关.
猜想3:可能与匀速拉动的速度大小和小车的重力都有关.
各小组分别根据各自的猜想进行了探究,实验记录如下表.
兰兰小组的实验记录
| 物理量 变化因素 | 小车重力/N | 绳端拉力/N | 机械效率 |
| 较小速度 | 10 | 4.2 | 79.4% |
| 较大速度 | 10 | 4.2 | 79.4% |
| 探究结果 | |||
| 物理量 变化因素 | 小车重力/N | 绳端拉力/N | 机械效率 |
| 大致相同的拉动速度 | 10 | 4.2 | 79.4% |
| 15 | 6.0 | ||
| 探究结果 | |||
(1)由图知,n=2,
∵不计摩擦,
∴F=
G,1 2
即:600N=
G,1 2
∴G=1200N;
故答案为:1200.
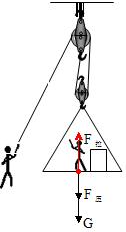
(2)吊蓝受到自身的重力、绳子的拉力、人和器材的压力的作用,作用点在吊篮底部的中心上,过作用点分别作出这三个力,如下图所示:
(3)W有=Gh=(m人+m器材)gh=(60kg+20kg)×10N/kg×10m=8000J,
s=2h=2×10m=20m,
W总=Fs=500N×20m=10000J,
η=
=W有用 W总
×100%=80%.8000J 10000J
答:这个滑轮组的机械效率是80%.
(4)①芳芳第1次实验中:η=
,代入相关数据,Gh FS
∴斜面高度和长度的比值:
=h S
=ηF G
=0.3334879.4%×4.2N 10N
∴第2次实验的机械效率:η′=
×G′ F′
=h S
×0.33348×100%=83.37%15N 6.0N
②兰兰小组:由表格中数据知,两次被提升小车的重力相同,第二次比第一次提升的速度大,两次测量的机械效率相同,所以可以看出机械效率与物体被提升的高度无关.
芳芳小组:两次实验物体被提升的速度相同,第二次提升小车的重力大,机械效率也高,所以可以看出机械效率与被提升物体的重力有关.
故答案为:
兰兰小组的实验记录
| 物理量 变化因素 | 小车重力/N | 绳端拉力/N | 机械效率 |
| 较小速度 | 10 | 4.2 | 79.4% |
| 较大速度 | 10 | 4.2 | 79.4% |
| 探究结果 | 机械效率的大小与拉动的速度的大小无关 | ||
| 物理量 变化因素 | 小车重力/N | 绳端拉力/N | 机械效率 |
| 大致相同的拉动速度 | 10 | 4.2 | 79.4% |
| 15 | 6.0 | 83.37% | |
| 探究结果 | 机械效率的大小与物重的大小有关 | ||
