问题
选择题
在直角梯形ABCD中,AD∥BC,AB⊥BC,E是CD的中点,且AB=AD+BC,△ABE是( )
A.等腰三角形
B.等腰直角三角形
C.直角三角形
D.等边三角形
答案
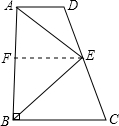
过E点作EF∥AD,
∵AD⊥AB
∴EF⊥AB
∵E为CD的中点
∴EF是梯形ABCD的中位线
∴2EF=AD+BC,EF是线段AB的垂直平分线,
∵AF=BF,AB=AD+BC,即EF=
AB,AE=BE,1 2
∴∠AEB是直角
即△ABE是等腰直角三角形.
故选B.
