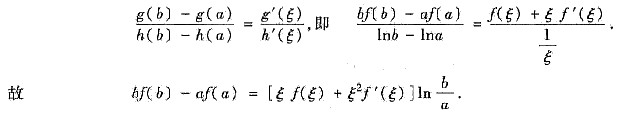问题
问答题
设0＜a＜b，f(x)在[a，b]上连续，在(a，b)内可导，证明：在(a，b)内至少存在一点ξ，使得
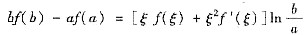
答案
参考答案：[证法一] 令
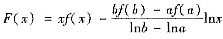，则F(x)在[a，b]上连续，在(a，b)内可导．由于
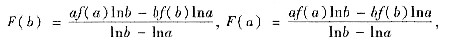
所以F(a)=F(b)．根据岁尔定理可得：在(a，b)内至少存在一点ξ，使得F’(ξ)=0，即
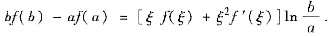
[证法二] 令g(x)=xf(x)，h(x)=lnx，则g(x)，h(x)在[a，b]上满足柯两中值定理条件，所以存在ξ∈(a，b)，使得
