参考答案：D

解析： 对于(A)：f(x)在[a，6]连续

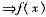在[a，b]达到最大值与最小值．由f(a)≥f(b)，若f(x)的最大值在区间端点达到，则必在x=a达到，由f(x)的可导性，必有

＞0表明f(x)的最大值不能在端点达到，同理可证f(x)的最小值也不能在端点x=a或x=b达到，因此f(x)在[a，b]的最大值与最小值必在开区间(a，b)达到，又f(x)在[a，b]可导，在最大值点与最小值点处f’(x)=0，所以f’(x)在(a，b)至少

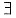两个零点．故(A)正确．
对于(B)：由f"(x)＞0(x∈(a，b))及f’(x₀)=0可判断f’(x)在x₀两侧的符号，从而可得f(x)在x=x₀两侧的升降性．
由

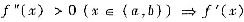在(a，b)单调上升

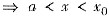时f’(x)＜f’(x₀)=0；x₀＜x＜b时0=f’(x₀)＜f’(x)

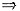x∈(a，x₀]时f(x)单调下降，x∈[x₀，b)时f(x)单调上升

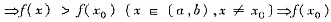是f(x)在(a，b)的最小值．
f’(a)＜0，f’(x₀))=0时类似可证f(x₀)是f(x)在(a，b)的最大值．故(B)正确．
对于(C)：设x=x₀是极小值点，若它不是最小值点，直观上看，还应存在一个极大值点，见图2-3．现证明之．

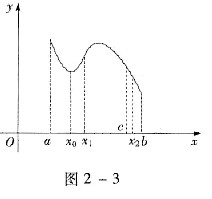
若f(x₀)不是f(x)在(a，b)的最小值，则]x₂∈(a，b)，f(x₂)＜f(x₀)，不妨设x₂＞x₀．由x=x₀是极小值点

，使得f(x₁)＞f(x₀)．再由连续函数中间值定理，

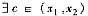使得f(C)=f(x₀)．现考察f(x)在区间[x₀，c]的值．

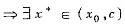，使得

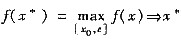是f(x)的极大值点，与f(x)在(a，b)有唯一极值点矛盾．因此f(x₀)是f(x)在(a，b)的最小值．故(C)正确．
[评注] ①请同学证明：设f(x)在[a，b]有连续的导数，在(a，b)有唯一驻点x=x₀，若f’₊(a)＞0(＜0)，f’_-(b)＜0(＞0)，则x=x₀是f(x)在[a，b]的最大值点(最小值点)．
②设x=a是y=f(x)在[a，b]上的最大(小)值点，又

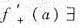，则f’₊(a)≤0(≥0)．
[分析与证明] 按f’₊(a)的定义，最大值(最小值)的定义及极限的不等式性质可得证．
注意，f(a)是f(x)在[a，b]的最大(小)值

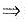
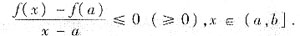
于是由f’₊(a)的定义及极限的不等式性质

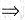
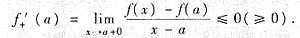
对于(D)：显然不对．正确命题是：若函数f(x)在[a，b]上连续，且f(a)=f(b)，但

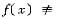C(常数)，则f(x)在(a，b)内必有最大值或最小值．
综上分析，应选(D)．