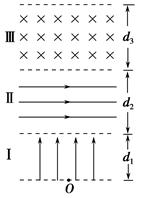
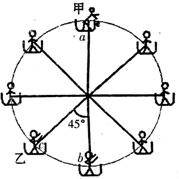
游乐园的小型“摩天轮”上对称站着质量均为m的8位同学,如图所示,“摩天轮”在竖直平面内逆时针匀速转动,若某时刻转到顶点a上的甲同学让一小重物做自由落体运动,并立即通知下面的同学接住,结果重物掉落时正处在c处(如图)的乙同学恰好在第一次到达最低点b处接到,己知“摩天轮”半径为R,重力加速度为g,(不计人和吊篮的大小及重物的质量).问:
(1)接住前重物下落运动的时间t=?
(2)人和吊篮随“摩天轮”运动的线速度大小v=?
(3)乙同学在最低点处对地板的压力FN=?
(1)由运动学公式2R=
gt2得,1 2
t=2
.R g
(2)由v=
得,s t
v=
=
×2πR1 8 t πR 8
=g R
π1 8
.gR
(3)设支持力为F,由牛顿第二定律得:F-mg=mv2 R
解得F=m(g+
g)=(1+π2 64
)mgπ2 64
由牛顿第三定律得人对地板的压力FN=(1+
)mg,方向竖直向下.π2 64
答:接住前重物下落运动的时间为2
.R g
(2)人和吊篮随“摩天轮”运动的线速度大小为
π1 8
.gR
(3)乙同学在最低点处对地板的压力FN=(1+
)mg.π2 64

 ×105 V/m,方向水平向右,Ⅲ区域磁感应强度B=5.0 T,方向垂直纸面向里,三个区域宽度分别为d1=5.0 m,d2=4.0 m,d3=
×105 V/m,方向水平向右,Ⅲ区域磁感应强度B=5.0 T,方向垂直纸面向里,三个区域宽度分别为d1=5.0 m,d2=4.0 m,d3=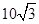 m.一质量m=1.0×10-8 kg、电荷量q=1.6×10-6C的粒子从O点由静止释放,粒子重力忽略不计.求:
m.一质量m=1.0×10-8 kg、电荷量q=1.6×10-6C的粒子从O点由静止释放,粒子重力忽略不计.求: