问题
计算题
如图所示空间分为Ⅰ，Ⅱ，Ⅲ三个足够长的区域，各边界面相互平行，其中Ⅰ，Ⅱ区域存在匀强电场EI＝1.0×104 V/m，方向垂直边界面竖直向上；EⅡ＝
×105 V/m，方向水平向右，Ⅲ区域磁感应强度B＝5.0 T，方向垂直纸面向里，三个区域宽度分别为d1＝5.0 m，d2＝4.0 m，d3＝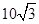
m．一质量m＝1.0×10－8 kg、电荷量q＝1.6×10－6C的粒子从O点由静止释放，粒子重力忽略不计．求：
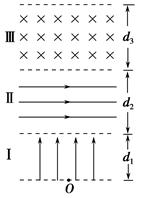
(1)粒子离开区域Ⅰ时的速度大小；
(2)粒子从区域Ⅱ进入区域Ⅲ时的速度方向与边界面的夹角；
(3)粒子从O点开始到离开Ⅲ区域时所用的时间．
答案
(1) v1＝4×103 m/s (2) θ＝30° (3)6.12×10-3s
题目分析：(1)由动能定理得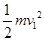 
＝qEId1 ① （2分）
得：v1＝4×103 m/s ② （1分）
(2)粒子在区域Ⅱ做类平抛运动．水平向右为y轴，竖直向上为x轴．设粒子进入区域Ⅲ时速度与边界的夹角为θ
tan θ＝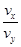
③（1分）
vx＝v1 vy＝at ④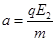（1分）
⑤（1分）
t＝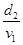
⑥（1分）
把数值代入得θ＝30°⑦（1分）
(3)粒子进入磁场时的速度v2＝2v1 ⑧（1分）
粒子在磁场中运动的半径R＝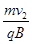
＝10m ⑨（1分）
粒子在磁场中运动所对的圆心角为120° 因此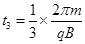
（1分）
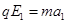
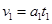（两式共1分）
由（2）得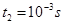
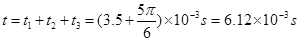（1+1=2分）