问题
计算题
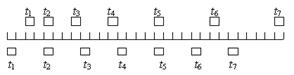
如图 所示,物体A的质量m1=1kg，静止在光滑水平面上的木板B的质量为m2=0.5kg、长l=1m，某时刻A以v0=4m/s的初速度滑上木板B的上表面，为使A不致于从B上滑落，在A滑上B的同时，给B施加一个水平向右的拉力F，若A与B之间的动摩擦因数μ=0.2，试求拉力F应满足的条件。（忽略物体A的大小）
答案
１Ｎ≤Ｆ≤３Ｎ
物体A滑上木板B以后，作匀减速运动，加速度a=μg，木板B作加速运动，有：
F+μm1g=m2aB 。物体Ａ不滑落的临界条件是Ａ到达Ｂ的右端时，Ａ、Ｂ具有共同的vt，则：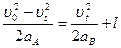
且：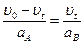
由此可得：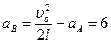
（m/s2） 代入得：Ｆ＝m2aB-μm1g=0.5×6-0.2×1×10=1(N)
若Ｆ<1N，则Ａ滑到Ｂ的右端时，速度仍大于Ｂ的速度，于是将从Ｂ上滑落，所以Ｆ必须大于等于１Ｎ。
当Ｆ较大时，在Ａ到达Ｂ的右端之前，就与Ｂ具有相同的速度，之后，Ａ必须相对Ｂ静止，才能不会从Ｂ的左端滑落。即有：
Ｆ＝（mA+mB）a
μmAg=mAa
所以：Ｆ="3N " 若Ｆ大于３Ｎ，Ａ就会相对Ｂ向左滑下。
综上：力Ｆ应满足的条件是：１Ｎ≤Ｆ≤３Ｎ