问题
问答题
某商场购进一批单价为16元的日用品,经试验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y
(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润每月的最大利润是多少
答案
参考答案:
依题意设y=kx+b,则有
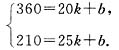
解得是k=30,b=960.
∴y=-30x+960(16≤x≤32).
(2)每月获得利润P=(-30x+960)(x-16)=30(-x2+48x-512)=-30(x-24)2+1920.
∴当x=24时,P有最大值,最大值为1920.即当价格为24元,每月才能获得最大利润1920元.
