问题
问答题
已知f(x),g(x)连续可导,且f’(x)=g(x),g’(x)=f(x)+φ(x),其中φ(x)为某已知连续函数,g(x)满足微分方程g’(x)-xg(x)=cosx+φ(x),求不定积分
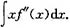
答案
参考答案:[*]
又由f’(x)=g(x),g’(x)=-f(x)+φ(x),有
[*]
解析:
[分析]: 由于积分中含有f"(x),可考虑用分部积分法。
[评注] 本题似乎应先解方程得f(x)再求积分,但由于φ(x)不是具体函数,所以不能直接解方程。
