问题
问答题
已知函数f(x)=-x3+ax2+bx+c图像上的点P(1，-2)处的切线方程为y=-3x+1.
(1)若函数f(x)在x=-2时有极值，求f(x)的表达式；
(2)函数f(x)在区间[-2，0]上单调递增，求实数b的取值范围，
答案
参考答案：
f′(x)=-3x2+2ax+b，
∵函数f(x)在z-1处的切线斜率为-3，∴f(1)=-3+2a+b=-3，即2a+b=0
又f(1)=-1+a+b+c=-2，得a+b+c=-1．
(1)函数f(x)在x=-2时有极值，所以f′(-2)=-12-4a+b=0，
解得a=-2，b=4，c=-3，
所以f(x)=-x3-2x2+4x-3.
(2)因为函数f(x)在区间[-2，0]上单调递增，所以导函数f′(x)=-3x2-bx+b在区间[-2，0]上的值恒大于或等于零，
则
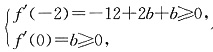得b≥4，所以实数6的取值范围为[4，+∞)．