问题
问答题
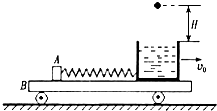
如图所示,光滑水平面上有一小车B,右端固定一砂箱,砂箱左侧连接一水平轻弹簧,小车和砂箱的总质量为M,车上放一小物体A,质量也是M,小物体A随小车以速度v0向右匀速运动,此时弹簧处于自由长度状态(小物体A与弹簧没有连接).小物体A与左侧车面间有摩擦,动摩擦因数为μ,与其它车面间无摩擦,在匀速运动时,距砂面H高处有一质量为m的泥球自由下落,恰好落在砂箱中.求:
(1)小车在前进中,弹簧弹性势能的最大值?
(2)为使小物体A不从车上滑下,车面粗糙部分至少应为多长?
答案
(1)小球掉入小车的过程小球与车水平方向的动量守恒
Mv0=(M+m)v1
弹簧的压缩量最大时,设共同速度为v2,则有
Mv0+(M+m)v1=(2M+m)v2
由能量转化和守恒关系有
Ep=
M1 2
+v 20
(M+m)1 2
-v 21
(2M+m)1 2 v 22
解以上方程,得Ep=Mm2v 20 2(M+m)(2M+m)
(2)根据功能关系有
μMgL=EP
L=m2v 20 2μ(M+m)(2M+m)g
答:(1)小车在前进中,弹簧弹性势能的最大值是Mm2v 20 2(M+m)(2M+m)
(2)为使小物体A不从车上滑下,车面粗糙部分至少应为m2v 20 2μ(M+m)(2M+m)g
