问题
解答题
已知直线l1：mx+8y+n=0，l2：2x+my﹣1=0，分别满足下列情况：
（1）两条直线相较于点P（m，﹣1）；
（2）两直线平行；
（3）两直线垂直，且l1在y轴上的截距为﹣1，试分别确定m，n的值．
答案
解：（1）由点P在直线l1，l2上，故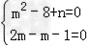
，
所以m=1，n=7．
（2）因为l1∥l2，且斜率存在，则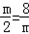
，∴m=±4．
又当m=4，n=﹣2时，两直线重合，当m=﹣4，n=2，同样
∴当m=4，n≠2或m=﹣4，n≠2时，两直线平行．
（3）当m=0时直线l1：y=﹣
和l2：x=
此时，l1⊥l2，
又l1在y轴上的截距为﹣1，n=8，
当m≠0时此时两直线的斜率之积等于
显然 l1与l2不垂直，
所以当m=0，n=8时，直线 l1 和 l2垂直满足题意．