问题
解答题
判断下列命题是全称命题还是特称命题，并判断其真假．
(1) 每个二次函数图象的开口都向下；
(2) 对任意一个实数x ，x2+x+1>0;
(3) 存在一个四边形不是平行四边形；
(4) 存在实数α、β ，使sin( α+ β)=sin α+sin β
答案
解：(1)全称命题．命题为假命题，如函数y=2x2的图象开口向上．
(2)全称命题．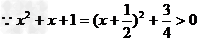
，∴命题为真命题．
(3)特称命题．∵梯形不是平行四边形，∴命题为真命题．
(4)特称命题．∵当α=β=0时，sin(α+β)=sinα+sinβ=0，∴命题为真命题．