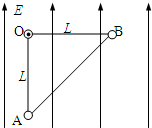
如图所示,两个带电小球(可视为质点),固定在轻质绝缘等腰直角三角形框架OAB的两个端点A、B上,整个装置可以绕过O点且垂直于纸面的水平轴在竖直平面内自由转动.直角三角形的直角边长为L.质量分别为mA=3m,mB=m,电荷量分别为QA=-q,QB=+q.重力加速度为g.
(1)若施加竖直向上的匀强电场E,使框架OB边水平、OA边竖直并保持静止状态,则电场强度E多大?
(2)若将匀强电场方向改为与原电场方向相反,保持E的大小不变,则框架OAB在接下来的运动过程中,带电小球A的最大动能EkA为多少?
(3)在(2)中,设以O点为零势能位,则框架OAB在运动过程中,A、B小球电势能之和的最小值E′为多少?
(1)以O为支点,根据三角架力矩平衡,M顺=M逆
mgL=qEL
求得E=mg q
(2)设OA边与竖直方向成α,当系统的力矩平衡时动能最大,则有 M顺=M逆
即 3mgLsinα=mgLcosα+qELcosα+qELsinα
解得,OA杆与竖直方向夹角α=45°时A球动能最大.
根据系统动能定理W合=△EK,得
-3mgL(1-cos45°)+mgLsin45°+qEL sin45°+qEL(1-cos45°)=
•4mv21 2
求得A球最大速度v=(
-1)gL2
得到A球动能EKA=
.3mgL(
-1)2 2
(3)设OA边与竖直方向成α时系统的速度为零,根据系统动能定理
-3mgL(1-cosα)+mgLsinα+qELsinα+qEL(1-cosα)=0
得α=90°时系统速度为零,不能再继续转过去了.
由于该过程电场力一直做正功,A、B小球电势能之和一直减小,所以此处A、B小球电势能之和最小,E′=-qEL=-mgL.
答:
(1)电场强度E是
.mg q
(2)框架OAB在接下来的运动过程中,带电小球A的最大动能EkA为
.3mgL(
-1)2 2
(3)框架OAB在运动过程中,A、B小球电势能之和的最小值E′为-mgL.
