问题
问答题
设某产品的产量Q与两种原料的投入量x，y的函数关系为
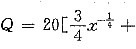
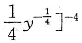，该产品的成本函数为C=4x+3y．
(Ⅰ) 若限定成本预算为80，计算使产量达到最高的原料投入量x和y；
(Ⅱ) 若限定产量为120，计算使成本最低的原料投入量x和y．
答案
参考答案：[分析与求解] (Ⅰ) 问题是求产餐函数Q在条件4x+3y=80下的最大值点．由[*]可得
[*]
因[*]是递减函数，当其达到最小值时Q达到最大值．为计算简便，计算[*]的最小值点．
记拉格朗日函数为
[*]
由
[*]
得
[*]
由实际问题Q存在最大值，因此所求的驻点，就是Q最大值点．
(Ⅱ) 由题设约束条件是
[*]
简化上式得
[*]
问题是求成本函数C在条件[*]下的最小值点．
作拉格朗日函数
[*]
由
[*]
得
[*]
是唯一的驻点，又由实际问题，成本函数存在最小值，因此所求的驻点就是最小值点．