问题
多项选择题
设f(x,y)在(0,0)连续,给定
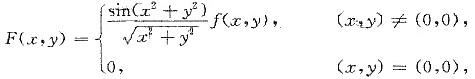
讨论F(x,y)在(0,0)点的可微性,若可微请求出F(x,y)在点(0,0)的全微分.
答案
参考答案:[分析与求解] 由于f(x,y)没给出具体的表达式,除了在(0,0)点连续外无其他条件,因此需要直接从定义出发来判断.
[*]
[*] 当f(0,0)=0时,[*]
当f(0,0)≠0时,[*]不存在.
同理
当f(0,0)=0时,[*]
当f(0,0)≠0时[*]不存在.
因为若F(x,y)在(0,0)可微,必有[*]存在,上述讨论表明,f(0,0)≠0时F(x,y)在(0,0)不可微.
下设f(0,0)=0,此时,[*]
按可微性定义,只须考察
[*]
其中 [*]
因此,当f(0,0)=0时,F(x,y)在(0,0)可微
且 [*]
解析:[*]
[*]
