问题
问答题
设函数y=y(x)在(-∞，+∞)有二阶导数且y＇≠0，x=x(y)是y=y(x)的反函数．
(Ⅰ) 试将x=x(y)所满足的微分方程
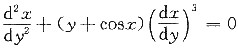变换为y=y(x)所满足的微分方程；
(Ⅱ) 求变换后的微分方程满足初始条件
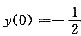，y＇(0)=2的解；
(Ⅲ) 请验证，对所求的y=y(x)在(-∞，+∞)存在反函数．
答案
参考答案：[分析与求解] (Ⅰ) 这实质上是求反函数的一、二阶导数的问题，由反函数求导公式知
[*]
代入原微分方程得
[*]
即二阶线性常系数非齐次方程
[*]
(Ⅱ) 该方程的特征方程是λ2-1=0，特征根λ1，2=±1，由于非齐次项cosβx，β=1，βi=i≠λ1，2，则设①的特解是
y=Acosx+Bsinx
代入①得
-2Acosx-2Bsinx=cosx
求得
[*]
即①有特解 [*]于是①的通解是
[*]
又由初始条件得c1=1，c2=-1，因此所求的解为
[*]
(Ⅲ) 对y(x)=ex-e-x-[*] (x∈(-∞，+∞))求导得
[*]
y(x)在(-∞，+∞)单调上升 [*] y(x)在(-∞，+∞)存在反函数．