A股票和B股票在5种不同经济状况下预期报酬率的概率分布如下表所示:
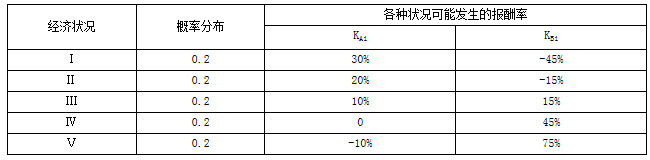
要求:
(1) 分别计算A股票和B股票报酬率的期望值及其标准离差;
(2) 假设A股票和B股票收益率的相关系数为-1,计算A股票和B股票报酬率的协方差;
(3) 根据(2)计算A股票和B股票在不同投资比例下投资组合的预期报酬率和标准离差。

(4) 已知A股票的必要收益率为10%,市场组合的收益率为12%,无风险收益率为 4%,则A股票的β系数为多少
参考答案:
(1) A股票报酬率的预期值=0.2×0.3+0.2×0.2+0.2×0.1+0.2×0+0.2×(-0.1)=0.1=10%
B股票报酬率的预期值=0.2×(-0.45)+0.2×(-0.15)+0.2×0.15+0.2×0.45+0.2×0.75=0.15=15%
A股票报酬率的标准差σl;[(0.3-0.1)2×0.2+(0.2-0.1)2×0.2+(0.1-0.1)2×0.2+(0-0.1)2×0.2+(-0.1-0.1)2×0.2]1/2=14.14%
B股票报酬率的标准差σ2=[(-0.45-0.15)2×0.2+(-0.15-0.15)2×0.2+(0.15-0.15)2×0.2+(0.45-0.15)2×0.2+(0.75-0.15)2×0.2]1/2=42.43%
A股票报酬率的变化系数=14.14%/10%=1.414
B股票报酬率的变化系数=42.43%/15%=2.829
(2)
(3)A股票和B股票在不同投资比例下投资组合的期望报酬率和标准差

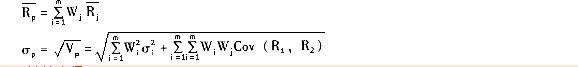
即可计算求得:
当W1=1,W2=0,组合的期望报酬率=1×10%+0×15%=10%
当W1=0.8,W2=0.2,组合的期望报酬率=0.8×10%+0.2×15%=11%
当相关系数=-1时,COV(R1,R2)=-σ1σ2
当W1=1,W2=0,组合的标准差
(4)根据资本资产定价模型: E(Ri)=RF+βi(Rm-RF) 即:10%=4%+β(12%-4%),所以,β=0.75
解析:
本题的主要考核点是第三章期望值、标准离差和第五章投资组合的收益率和标准离差的计算。
