问题
问答题
设A是n阶矩阵,证明:
1.r(A)=1的充分必要条件是存在n阶非零列向量α,β,使得A=αβT;
答案
参考答案:若r(A)=1,则A为非零矩阵且A的任意两行成比例,即
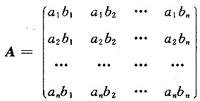
于是
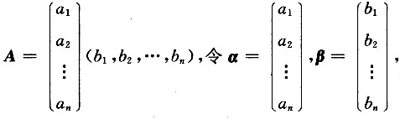 显然α,β都不是零向量且A=αβT;
显然α,β都不是零向量且A=αβT;
反之,若A=αβT,其中α,β都是n维非零列向量,则r(A)=r(αβT)≤r(α)=1,又因为α,β为非零列向量,所以A为非零矩阵,从而r(A)≥1,于是r(A)=1.
设A是n阶矩阵,证明:
1.r(A)=1的充分必要条件是存在n阶非零列向量α,β,使得A=αβT;
参考答案:若r(A)=1,则A为非零矩阵且A的任意两行成比例,即
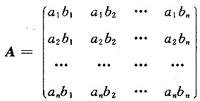
于是
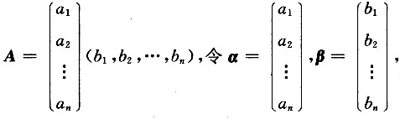 显然α,β都不是零向量且A=αβT;
显然α,β都不是零向量且A=αβT;
反之,若A=αβT,其中α,β都是n维非零列向量,则r(A)=r(αβT)≤r(α)=1,又因为α,β为非零列向量,所以A为非零矩阵,从而r(A)≥1,于是r(A)=1.