问题
选择题
已知命题p：m<0，命题q：∀x∈R，x2＋mx＋1>0成立，若“p∧q”为真命题，则实数m的取值范围是
A．[－2，0]
B．(0，2)
C．(－2，0)
D．(－2，2)
答案
答案：C
由∀x∈R，x2＋mx＋1>0成立，Δ＝m2－4<0，
所以－2<m<2.因为“p∧q”为真命题，则p，q都为真命题，
故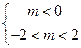
，即－2<m<0.
搜题请搜索小程序“爱下问搜题”
已知命题p：m<0，命题q：∀x∈R，x2＋mx＋1>0成立，若“p∧q”为真命题，则实数m的取值范围是
A．[－2，0]
B．(0，2)
C．(－2，0)
D．(－2，2)
答案：C
由∀x∈R，x2＋mx＋1>0成立，Δ＝m2－4<0，
所以－2<m<2.因为“p∧q”为真命题，则p，q都为真命题，
故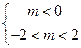，即－2<m<0.