问题
问答题
已知a0=3,a1=5,且对任何自然数n>1,
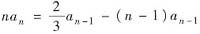 ,证明:当|x|<1时,幂级数
,证明:当|x|<1时,幂级数
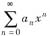 收敛,并求其和雨数.
收敛,并求其和雨数.
答案
参考答案:由题设[*],从而[*],所以幂级数收敛半径为R=1.故当|x|<1时,幂级数[*]绝对收敛.
令[*],则
[*]
即
[*]
解上述一阶线性微分方程得:[*],由条件S(0)=a0=3可确定[*],故该幂级数的和函数为
[*]
已知a0=3,a1=5,且对任何自然数n>1,
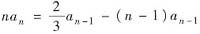 ,证明:当|x|<1时,幂级数
,证明:当|x|<1时,幂级数
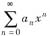 收敛,并求其和雨数.
收敛,并求其和雨数.
参考答案:由题设[*],从而[*],所以幂级数收敛半径为R=1.故当|x|<1时,幂级数[*]绝对收敛.
令[*],则
[*]
即
[*]
解上述一阶线性微分方程得:[*],由条件S(0)=a0=3可确定[*],故该幂级数的和函数为
[*]