问题
填空题
若x+y=12，求
|
答案
∵x+y=12，
∴y=12-x①，
将①代入
+x2+4
得，y2+9
+x2+4
②，(12-x)2+9
由②得，
+(x-0)2+(0-2)2
，(x-12)2+(0-2)2
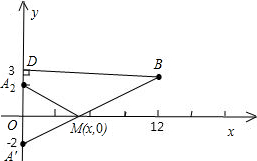
可理解为M（x，0）到A（0，2）和B（12，3）的距离的最小值．
作A关于轴的对称点A'（0，-2），连接A′B，与x轴交点即为M．
在Rt△A'DB中，A'B=
=A′D2+BD2
=13．52+122
故答案为：13．
如图：
