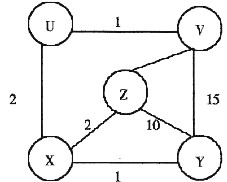
考虑下图所示的网络。假设每个节点初始时知道到其每个邻居的费用。考虑距离向量算法,说明节点Z的距离向量表表项(包括算法收敛过程中每次迭代所得的距离向量表)。
参考答案:本题考查的是“距离-向量路由算法”。
距离向量算法中,每个节点x维护如下的信息:
(1)Dx(y)为节点x到y的最小路径开销的估计值,y为网络中任意其它节点。
(2)每个节点维护着自己的距离向量:Dx=[Dx(y):y∈N](N为节点集合),其中记录着从节点x到任意节点的最短路径开销估计值。
(3)每个节点都保存着所有邻居的距离向量。
(4)每个节点维护到其邻居的链路开销c(x,v),v为x的邻居节点集合。
距离向量算法的基本思想:每个节点维护自己到所有节点的最短路径开销,即距离向量,每个节点定时向其邻居公告自己的距离向量。如果从邻居收到了新的距离向量,则重新利用B—F公式来计算自己的距离向量。如果重新计算后产生了新的距离向量网络其它,则向自己的邻居发送新的距离向量。B—F公式形式如下:
Dx(y)←minv{c(x,v)+Dv(y)}for each node y∈N,
其中minv是指取遍x的所有邻居。
距离向量算法具体如下:
对每个节点x:
Initialization:
for all destinati()ns v in N:
Dx(y)=c(x,y)/*if y is not a neighbor then c(x,y)=∞*/
for each neighbor w
Dw(y)=∞for all destination y in N
for each neighbor w
seild distance vector Dx=[Dx(y):y in N]to w
Loop
wait (until I see a link cost change to some rteighbor w or until I receive a distance vector from some neighbor w)
for each v in N:
Dx(y)=minv{c(x,v)+Dv(y)}
if Dx(y) changed for any destination y
send distance vector Dx=[Dx(y):Y in N]to all neighbors
Forever
根据题中所给出的图,首先进行节点初始化。对于节点Z,初始Dz(u)=∞;Dz(v)=5;Dz(x)=2;Dz(y)=10;Dz(z)=0;故初始时Dz=[∞,5,2,10,0]。Z除了要维护自己的距离向量外,还要保存邻居节点v、x、y的距离向量,根据算法可知,初始时保存在z中的Dv=Dx=Dy=[∞,∞,∞,∞,∞]。节点z的距离向量Dz以及z所保存的邻居节点的距离向量Dv、Dx、Dy共同组成节点z的距离向量表。其中每一行对应一个距离向量,行标指明其所属节点。由此z节点的初始距离向量表是
费用到
u v x y z
v ∞ ∞ ∞ ∞ ∞
x ∞ ∞ ∞ ∞ ∞
y ∞ ∞ ∞ ∞ ∞
z ∞ 5 2 10 0
按照相同的方法,对其他各节点的距离向量表进行初始化。其中v节点距离向量表中Dv=[1,0,∞,15,5];X节点距离向量表中Dx=[2,∞,0,1,2];Y节点距离向量表中Dy=[∞,15,1,0,10];
初始化后,每个节点向其邻居公告自己的距离向量,假设v,X,Y的距离向量公告同步到达z,Z根据收到的距离向量公告更新本节点所存储的邻居节点的距离向量。同时按B—F公式,对自己的距离向量进行更新,其中,
Dz(u)=min{c(z,v)+Dr(u),c(z,x)+Dx(u),c(z,y)+Dy(u)}={6,4,∞)=4;
Dz(v)=min{c(z,v)+Dv(v),c(z,x)+Dx(v),c(g,y)+Dy(v)}={5,∞,25)=5;
Dz(x)=min{c(z,v)+Dv(x),c(z,x)+Dx(x),c(z,y)+Dy(x)}={∞,2,11)=2;
Dz(y)=min{c(z,v)+Dv(y),c(z,x)+Dx(y),c(z,y)+Dy(y))=(20,3,10}=3;
Dz(z)=0;
Dz=[4,5,2,3,0]
所以,z节点的距离向量表更新为
费用到
u v x y z
v 1 0 ∞ 15 5
x 2 ∞ 0 1 2
y ∞ 15 1 0 10
z 4 5 2 3 0
其他节点在收到邻居节点传来的距离向量公告后,也要进行类似的更新操作。根据后,若本节点的距离向量发生变化,则再次将自身的距离向量公告给邻居节点。如此继续,直至所有节点的距离向量均不发生变化为止。在此过程中,z的距离向量表被逐次更新为
费用到
u v x y z
v 1 0 3 15 5
x 2 3 0 1 2
y 3 15 1 0 3
z 4 5 2 3 0
费用到
u v x y zv
1 0 3 4 5 x
2 3 0 1 2 y
3 4 1 0 3 z
4 5 2 3 0

